Sistem zecimal

Un sistem zecimal (de la latina medie decimalis , la latina decem "zece"), cunoscut și sub numele de sistemul zece sau sistem decadic , este un sistem numeric care folosește numărul 10 ca bază .

De regulă, se înțelege în mod specific sistemul zecimal cu sistem de valori plasate , care a fost dezvoltat în cifre indiene , transmis țărilor europene prin mediere arabă și este acum stabilit la nivel mondial ca standard internațional.

Cu toate acestea, sistemele zecimale sunt, de asemenea, sisteme numerice bazate pe 10 fără un sistem de valori de poziție, deoarece se bazează pe numerele multor limbaje naturale și numerele mai vechi , uneori în legătură cu sistemele numerice quinare , vigesimale sau alte .

Antropologic , apariția sistemelor zecimale - și a sistemelor chinare - este asociată cu cele două degete de 5 ori ale oamenilor . Acestea au servit drept ajutoare de numărare și aritmetice ( aritmetica degetelor ). Această explicație este susținută de cifre pentru 5 („mână”) și 10 („două mâini”) în mai multe limbi.

Sistem de valori locale zecimale

Cifre

Cele zece cifre sunt utilizate în sistemul zecimal

0 (zero) , 1 (unul) , 2 (două) , 3 (trei) , 4 (patru) , 5 (cinci) , 6 (șase) , 7 (șapte) , 8 (opt) , 9 (nouă) ,

denumit cifre zecimale .

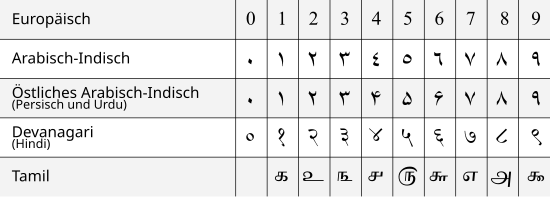
Cu toate acestea, aceste cifre sunt scrise diferit în diferite părți ale lumii.

Numeralele indiene sunt folosite și astăzi în diferitele scripturi indiene ( Devanagari , Bengali , Tamil , etc.). Sunt foarte diferiți unul de celălalt.

definiție

În lumea vorbitoare de limbă germană, un număr zecimal este de obicei sub formă

${\ displaystyle z_ {m} \, z_ {m-1} \, \ ldots \, z_ {0} \, \ operatorname {,} \, z _ {- 1} \, z _ {- 2} \, \ ldots \, z _ {- n} \ qquad \ left (m, n \ in \ mathbb {N} \ quad z_ {i} \ in \ {0, \ ldots, 9 \} \ right)}$

scris; În plus, există și alte ortografii în funcție de scopul și locația . Fiecare este unul dintre numerele menționate mai sus. Fiecare cifră are o valoare numerică și, în funcție de poziția sa, o valoare de poziție. Valoarea numerică este în ordinea convențională de numărare. Indicele determină valoarea, care este puterea a zece . Cifrele sunt scrise unul după altul , fără un separator, cu cifra cea mai semnificativă cu cifra de pe extrema stângă și cifra semnificativ mai mici cu cifre până la dreapta de ea în ordine descrescătoare. Pentru a reprezenta numere raționale cu dezvoltare non-periodică, cifrele de urmat după o virgulă separatoare . În lumea vorbitoare de limbă engleză, în locul virgulei se folosește un punct. ${\ displaystyle z_ {i}}$${\ displaystyle i}$${\ displaystyle 10 ^ {i}}$${\ displaystyle z_ {m}}$${\ displaystyle z_ {m-1}}$${\ displaystyle z_ {0}}$${\ displaystyle z _ {- 1}}$${\ displaystyle z _ {- n}}$

Valoarea numărului zecimal se obține astfel prin adunarea acestor cifre, care sunt înmulțite cu valoarea lor de poziție în prealabil; în plus, semnul trebuie pus în față; un semn lipsă înseamnă un plus: ${\ displaystyle Z}$

${\ displaystyle Z = \ sum _ {i = -n} ^ {m} z_ {i} \ cdot 10 ^ {i} \ geq 0 \; \ qquad Z = - \ sum _ {i = -n} ^ { m} z_ {i} \ cdot 10 ^ {i} \ leq 0}$.

Această reprezentare se mai numește dezvoltarea fracției zecimale .

Exemplu:

${\ displaystyle 7023 {,} 48 = 7 \ times 10 ^ {3} +0 \ times 10 ^ {2} +2 \ times 10 ^ {1} +3 \ times 10 ^ {0} +4 \ times 10 ^ {-1} +8 \ cdot 10 ^ {- 2}}$

Cu potențiale rezolvate, obținem:

${\ displaystyle 7023 {,} 48 = 7 \ cdot 1000 + 0 \ cdot 100 + 2 \ cdot 10 + 3 \ cdot 1 + 4 \ cdot 0 {,} 1 + 8 \ cdot 0 {,} 01}$

Dezvoltarea fracției zecimale (conversia numerelor zecimale periodice în fracții)

Cu ajutorul extinderii fracțiilor zecimale , puteți atribui o succesiune de cifre fiecărui număr real . Fiecare parte finită a acestei secvențe definește o fracție zecimală , care este o aproximare a numărului real. Numărul real în sine este obținut prin deplasarea de la sumele finite ale părților la seria infinită peste toate cifrele.

În mod formal, valoarea seriei este numită. ${\ displaystyle z = 0, a_ {1} a_ {2} a_ {3} \ ldots}$${\ displaystyle \ textstyle \ sum _ {i = 1} ^ {\ infty} a_ {i} 10 ^ {- i}}$

Se spune că dezvoltarea fracției zecimale se oprește când secvența de cifre dintr-o poziție n constă doar din zerouri, adică numărul real reprezentat este deja o fracție zecimală în sine. Mai ales cu toate numerele iraționale , succesiunea cifrelor nu se întrerupe; există o expansiune infinită a fracției zecimale.

Următoarele relații sunt utilizate pentru a transforma expansiunea periodică a fracțiilor zecimale :

${\ displaystyle 0 {,} {\ overline {1}} = {\ frac {1} {9}}; \ quad 0 {,} {\ overline {01}} = {\ frac {1} {99}} ; \ quad 0 {,} {\ overline {001}} = {\ frac {1} {999}}; \ quad \ ldots}$.

Aceste identități sunt evidente din regulile de calcul pentru seriile geometrice , care pentru aplicabile. În primul exemplu, se alege și nu începe însumarea până la primul termen din secvență. ${\ displaystyle \ textstyle \ sum _ {i = 0} ^ {\ infty} q ^ {i} = {\ frac {1} {1-q}}}$${\ displaystyle q <1}$${\ displaystyle q = 10 ^ {- 1}}$

Exemple:

${\ displaystyle 0 {,} 55555 \ ldots = 0 {,} {\ overline {5}} = {\ frac {5} {9}}}$

${\ displaystyle 0 {,} 33333 \ ldots = 0 {,} {\ overline {3}} = {\ frac {3} {9}} = {\ frac {1} {3}}}$

${\ displaystyle 0 {,} 424242 \ ldots = 0 {,} {\ overline {42}} = {\ frac {42} {99}} = {\ frac {14} {33}}}$

${\ displaystyle 0 {,} 081081081 \ ldots = 0 {,} {\ overline {081}} = {\ frac {81} {999}} = {\ frac {3} {37}}}$

Perioada este transferată la ghișeu în fiecare caz . În numitor sunt atât de multe cifre câte cifre sunt în perioada. Dacă este necesar, pauza rezultată ar trebui scurtată .

Calculul este puțin mai complicat dacă perioada nu urmează imediat punctul zecimal:

Exemple:

${\ displaystyle 0 {,} 83333 \ ldots = 0 {,} 8 {\ overline {3}} = 8 {,} {\ overline {3}}: 10 = \ left (8 + {\ frac {3} { 9}} \ right): 10 = \ left (8 + {\ frac {1} {3}} \ right): 10 = {\ frac {25} {3}}: 10 = {\ frac {25} { 30}} = {\ frac {5} {6}}}$

${\ displaystyle 0 {,} 492363636 \ ldots = 0 {,} 492 {\ overline {36}} = 492 {,} {\ overline {36}}: 1000 = 492 {\ frac {36} {99}}: 1000 = 492 {\ frac {4} {11}}: 1000 = {\ frac {5416} {11}}: 1000 = {\ frac {5416} {11000}} = {\ frac {677} {1375}} }$

${\ displaystyle 13 {,} 54323232 \ ldots = 13 {,} 54 {\ overline {32}}}$

Pasul 1: înmulțiți numărul de pornire cu o putere de zece astfel încât exact o perioadă (în exemplul 32) să fie în fața punctului zecimal:

${\ displaystyle x = 13 {,} 543232 \ ldots | \ cdot 10 {.} 000}$

${\ displaystyle 10 {.} 000 \ cdot x = 135 {.} 432 {,} 3232 \ ldots}$

Pasul 2: apoi înmulțești numărul de pornire cu o putere de zece, astfel încât punctele să înceapă exact după punctul zecimal:

${\ displaystyle x = 13 {,} 543232 \ ldots | \ cdot 100}$

${\ displaystyle 100 \ cdot x = 1 {.} 354 {,} 323232 \ ldots}$

Al treilea pas: scădeți cele două linii create de pasul 1 și 2 unul de celălalt: (punctele după punctul zecimal sunt omise)

${\ displaystyle 10 {.} 000 \ cdot x = 135 {.} 432 {,} 323232 \ ldots}$ (Linia 1)

${\ displaystyle 100 \ cdot x = 1354 {,} 323232 \ ldots}$ (Randul 2)

${\ displaystyle 9 {.} 900 \ cdot x = 135 {.} 432-1 {.} 354 = 134 {.} 078 \!}$ (Rândul 1 minus rândul 2)

Pasul 4: comutator

${\ displaystyle 9 {.} 900 \ cdot x = 134 {.} 078 |: 9 {.} 900}$

Rezultat: ${\ displaystyle x = {\ frac {134 {.} 078} {9 {.} 900}} = 13 {,} 54 {\ overline {32}}}$

Ambiguitatea reprezentării

O caracteristică specială a expansiunii fracției zecimale este că multe numere raționale au două expansiuni ale fracției zecimale diferite. După cum sa descris mai sus, se poate remodela și face afirmația ${\ displaystyle 0 {,} {\ overline {9}}}$

${\ displaystyle 0 {,} {\ overline {9}} = {\ frac {9} {9}} = 1}$

ajunge, vezi articolul 0.999 ...

Din această identitate se poate deduce în continuare că multe numere raționale (și anume toate cu expansiunea fracției zecimale finite, cu excepția lui 0) pot fi reprezentate în două moduri diferite: fie ca o fracție zecimală finită cu perioada 0, fie ca o fracție zecimală infinită cu perioada 9. Pentru a face reprezentarea fără echivoc Pentru a face acest lucru, puteți interzice pur și simplu perioada 9 (sau mai rar perioada 0).

formulă

Următoarea formulă poate fi configurată pentru fracții zecimale periodice cu un zero în fața punctului zecimal:

${\ displaystyle p = {\ frac {x \ cdot \ left (10 ^ {n} -1 \ right) + y} {10 ^ {m} \ cdot \ left (10 ^ {n} -1 \ right)} }}$

Aici p este numărul, x este numărul înainte de începutul perioadei (ca număr întreg), m este numărul de cifre înainte de începutul perioadei, y este secvența cifrelor perioadei (ca număr întreg) și n este lungimea perioadei.

Aplicarea acestei formule trebuie demonstrată folosind ultimul exemplu:

${\ displaystyle p = 0 {,} 492363636 \ ldots = 0 {,} 492 {\ overline {36}}}$

${\ displaystyle x = 492; \ quad m = 3; \ quad y = 36; \ quad n = 2}$

${\ displaystyle p = {\ frac {x \ cdot \ left (10 ^ {n} -1 \ right) + y} {10 ^ {m} \ cdot \ left (10 ^ {n} -1 \ right)} } = {\ frac {492 \ cdot \ left (10 ^ {2} -1 \ right) +36} {10 ^ {3} \ cdot \ left (10 ^ {2} -1 \ right)}} = { \ frac {492 \ cdot 99 + 36} {1000 \ cdot 99}} = {\ frac {48744} {99000}} = {\ frac {677} {1375}}}$

perioadă

În matematică , perioada unei fracții zecimale este o cifră sau o secvență de cifre care se repetă iar și iar după punctul zecimal. Toate numerele raționale și numai acestea au o expansiune periodică a fracțiilor zecimale.

Exemple:

Pur periodic: (perioada începe imediat după punctul zecimal)

1/3 = 0 3 3333 ...

1/7 = 0, 142857 142857 ...

1/9 = 0, 1 1111 ...

Periodic mixt: (după punctul zecimal există o perioadă anterioară înainte ca perioada să înceapă)

2/55 = 0,0 36 363636 ... (perioada anterioară 0; lungimea perioadei 2)

1/30 = 0,0 3 333 ... (perioada anterioară 0; lungimea perioadei 1)

1/6 = 0,1 6 666 ... (perioada anterioară 1; lungimea perioadei 1)

134078/9900 = 13,54 32 32 ... (perioada anterioară este de 54; lungimea perioadei este de 2)

Fracțiile zecimale finite se numără și între fracțiile zecimale periodice; după introducerea unui număr infinit de zerouri, de exemplu 0,12 = 0,12000 ...

Perioadele reale (adică fără fracții zecimale finite) apar în sistemul zecimal exact când numitorul fracției subiacente nu poate fi generat exclusiv de factorii primi 2 și 5. 2 și 5 sunt factorii primi ai numărului 10, baza sistemului zecimal. Dacă numitorul este un număr prim (cu excepția 2 și 5), perioada are cel mult o lungime care este cu una mai mică decât valoarea numitorului (prezentată cu caractere aldine în exemple). ${\ displaystyle p}$

Lungimea exactă a perioadei (dacă numărul prim este nici 2 , nici 5) corespunde cel mai mic număr natural , în care prim factorizarea de loc. ${\ displaystyle 1 / p}$${\ displaystyle n}$${\ displaystyle p}$${\ displaystyle R_ {n} = {10 ^ {n} -1}}$

Exemplu pentru lungimea perioadei 6 : (10 ⁶ - 1) = 999.999:

999.999 = 3 x 3 x 3 x 7 · 11 · 13 · 37 1/ 7 = 0 142857 142857 ... si 1/ 13 = 0, 076 923 076 923 ...

Atât 1/7, cât și 1/13 au o perioadă de 6, deoarece 7 și 13 apar pentru prima dată în factorizarea primă de 10 ⁶ - 1. Cu toate acestea, 1/37 are o perioadă de doar 3, deoarece deja (10 ³ - 1) = 999 = 3 · 3 · 3 · 37.

Dacă numitorul nu este un număr prim, lungimea perioadei rezultă în consecință ca numărul pentru care numitorul este divizor pentru prima dată ; factorii primi 2 și 5 ai numitorului nu sunt luați în considerare. ${\ displaystyle n}$${\ displaystyle R_ {n} = {10 ^ {n} -1}}$

Exemple: 1/185 = 1 / (5 * 37) are aceeași lungime de perioadă ca 1/37, și anume 3.

1/143 = 1 / (11 13) are lungimea perioadei 6, deoarece 999.999 = 3 3 3 7 143 37 (vezi mai sus)

1/260 = 1 / (2 · 2 · 5 · 13) are aceeași lungime de perioadă ca 1/13, adică 6.

Pentru a determina în mod eficient lungimea perioadei , determinarea factorizării prime a secvenței numerice în creștere rapidă 9, 99, 999, 9999 etc. poate fi evitată folosind relația echivalentă , adică multiplicarea repetată (începând cu 1) cu 10 modulo numitorul dat , până când acesta este din nou egal cu 1. De exemplu pentru : ${\ displaystyle n}$${\ displaystyle 10 ^ {n} \ equiv 1 {\ pmod {k}}}$${\ displaystyle k}$${\ displaystyle k = 13}$

${\ displaystyle 10 ^ {1} \ equiv 10 {\ pmod {13}}}$,

${\ displaystyle 10 ^ {2} \ equiv 10 \ cdot 10 \ equiv 100 \ equiv 9 {\ pmod {13}}}$,

${\ displaystyle 10 ^ {3} \ equiv 9 \ cdot 10 \ equiv 90 \ equiv 12 {\ pmod {13}}}$,

${\ displaystyle 10 ^ {4} \ equiv 12 \ cdot 10 \ equiv 120 \ equiv 3 {\ pmod {13}}}$,

${\ displaystyle 10 ^ {5} \ equiv 3 \ cdot 10 \ equiv 30 \ equiv 4 {\ pmod {13}}}$,

${\ displaystyle 10 ^ {6} \ equiv 4 \ cdot 10 \ equiv 40 \ equiv 1 {\ pmod {13}}}$,

deci 1/13 are lungimea perioadei 6.

notaţie

Pentru fracțiile zecimale periodice, este comună o notație în care partea repetată periodic a zecimalelor este marcată printr-o linie . exemple sunt

• ${\ displaystyle 1/6 = 0 {,} 1 {\ bar {6}}}$,
• ${\ displaystyle 1/7 = 0 {,} {\ overline {142857}}}$.

Datorită limitărilor tehnice, există și alte convenții. Linia superioară poate fi plasată în față, accentul tipografic (aldin, cursiv, subliniat) al părții periodice poate fi selectat sau poate fi pus între paranteze:

• 1/6 = 0.1¯6 = 0.1 6 = 0.1 6 = 0.1 6 = 0.1 (6)
• 1/7 = 0, ¯142857 = 0, 142857 = 0, 142857 = 0, 142857 = 0, (142857)

Secvență non-periodică de cifre după punctul zecimal

Așa cum se explică în sistemul de valori de poziție al articolului , numerele iraționale (de asemenea) din sistemul zecimal au o secvență infinită, non-periodică de cifre după punctul zecimal. Numerele iraționale nu pot fi reprezentate printr-o secvență finită sau periodică de cifre. Se poate aborda cu fracții zecimale finite (sau periodice) după dorință, dar o astfel de reprezentare finită nu este niciodată exactă. Deci, este posibil doar cu ajutorul unor simboluri suplimentare să se indice numere iraționale prin reprezentări finite.

Exemple de astfel de simboluri sunt simboluri radicale , cum ar fi pentru , litere precum π sau e , precum și expresii matematice, cum ar fi serie infinită sau valori limită . ${\ displaystyle {\ sqrt {2}}}$

Conversia în alte sisteme de valori locale

Metodele de conversie de la și către sistemul zecimal sunt descrise în articolele despre alte sisteme de valori de poziție și sub schimbarea numărului de bază și sistemul de valori de poziție .

poveste

Una dintre cele mai vechi dovezi ale culturilor zecimale vorschriftlicher găsite într-un tezaur de Oberding de la începutul epocii bronzului (în jurul anului 1650 v. Chr.) Cu 791 bare de cupru standardizate în mare parte din Salzburg și Slovacia. Majoritatea acestor bare au fost plasate în grupuri de câte 10 câte 10 pachete.

Sistemele numerice zecimale - încă fără un sistem de valori locale și fără reprezentarea zerourilor - au stat la baza scripturilor numerice ale egiptenilor , minoicilor , grecilor și romanilor, printre altele . Acestea erau fonturi de numere adiționale , cu care numerele puteau fi scrise ca un ajutor de memorie atunci când se calculează , dar operațiunile aritmetice nu puteau fi efectuate în esență în scris: acestea erau mai degrabă cu aritmetică mentală sau cu alte ajutoare, cum ar fi calculul pietrelor ( psephoi grecesc , Calculi latini , în Evul Mediu târziu numit și banii aritmetici sau cipuri franceze ) pe aritmetica pe linii și, eventual, cu numerele degetelor .

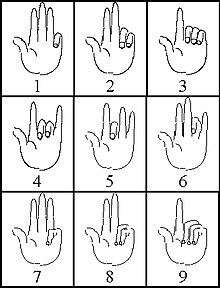
Numerele degetelor, care erau răspândite în epoca romană și medievală și utilizate, de asemenea, într-o formă ușor diferită în lumea arabă, se bazau pe un sistem zecimal pentru reprezentarea numerelor de la 1 la 9999, fără un simbol pentru zero și cu un sistemul de poziționare a propriilor poziții ale degetelor pe mâna stângă cu degetul mic, inelar și mijlociu unitățile 1 la 9 și cu degetul arătător și degetul mare zecile de la 10 la 90, în timp ce pe mâna dreaptă sutele cu degetul mare și arătătorul sunt un imaginea în oglindă a zecilor și a miilor cu cele trei degete rămase au fost prezentate ca o imagine în oglindă a celor. Se spune că aceste numere de degete au fost utilizate nu numai pentru numărarea și memorarea numerelor, ci și pentru aritmetică; Cu toate acestea, sursele scrise contemporane se limitează la descrierea pozițiilor degetelor și nu oferă informații mai detaliate despre operațiile matematice care pot fi efectuate cu acestea.

Pe abacul antichității greco-romane și al evului mediu creștin, pe de altă parte, era disponibil un sistem complet complet de valori zecimale pentru reprezentarea numerelor întregi, în sensul că pentru un număr dat numărul acestora, zeci, sute etc. a fost reprezentată prin calcularea pietrelor în coloane zecimale verticale corespunzătoare. Pe vechiul abac, acest lucru se făcea prin plasarea sau împingerea unui număr corespunzător de calcule în coloana zecimală respectivă, prin care se practica și un pachet de cinci, fiecare dintre cinci unități fiind reprezentat printr-un singur calcul într-o zonă specială laterală sau în partea de sus a coloanei zecimale. Pe abacul mănăstirii din Evul Mediu timpuriu, care astăzi este în mare parte asociat cu numele Gerberts și a fost utilizat în secolele X-XII, numărul unităților din coloana zecimală respectivă a fost reprezentat în schimb de o singură piatră, care este precedat de un număr de la 1 la 9 a fost numerotat, în timp ce Evul Mediu mai târziu și Epoca Modernă timpurie au revenit la utilizarea pietrelor aritmetice fără număr și a coloanelor sau acum linii trasate orizontal fie pentru aritmetica zecimală cu numere întregi la numărul de bază 10 (cu cinci pachete), sau pentru aritmetica financiară Unități monetare de bază moștenite de la monedă Carolingiană (1 balanță = 20 solidi = 240 denari) aliniate nedecimal. Pe versiunile antice și medievale ale acestui ajutor, valoarea zero a fost afișată lăsând necompletată coloana zecimală sau linia respectivă, și așa și pe abacul mănăstirii, pe care era disponibilă o piatră de calcul cu cifră arabă (cifra) pentru zero, dar a fost folosit în alte scopuri în operațiile aritmetice abazistice. Cu ajutorul abacului antic și medieval, adunarea și scăderea ar putea fi simplificate considerabil, în timp ce acestea nu erau foarte potrivite pentru înmulțire și împărțire sau necesitau operații relativ complicate, care au fost descrise mai ales pentru abacul mănăstirii în zonele medievale și erau notorii pentru dificultate.

Babilonienii au dezvoltat mai întâi un font numeric cu un sistem complet de valori de poziție, în care poziția semnului numeric determină și valoarea acestuia, bazată pe 60, și probabil că au adăugat un semn separat pentru zero încă din secolul al IV-lea î.Hr. Un font numeric cu un sistem de valori de poziție bazat pe 10, dar încă fără semn pentru zero, a fost creat probabil în China cu câteva secole înainte de începutul secolului (atestat în detalii încă din secolul al II-lea î.Hr.), probabil cu ajutorul a unei table de șah pe o tablă de șah chineză Varianta abacului și a fost completată doar de un simbol pentru zero sub influența indiană din secolul al VIII-lea.

În India însăși, începuturile sistemului zecimal pozițional cu caractere pentru zero nu pot fi determinate cu certitudine. Scrierea numerică Brahmi mai veche , care a fost utilizată între secolele III și VIII, a folosit un sistem zecimal cu abordări ale scrierii poziționale, dar încă fără un simbol pentru zero. Cea mai veche formă indiană a cifrelor indo-arabe de astăzi , cu simboluri de la 1 la 9 și un punct sau cerc mic pentru zero derivat din scrierea numărului Brahmi, este prima în afara Indiei din secolul al VII-lea în Asia de Sud-Est ca urmare a dovezilor epigrafice că poate fi datat în condiții de siguranță la exportul indian și poate fi documentat în India însăși încă din secolul al IX-lea; cu toate acestea, se crede că acest sistem numeric a început să fie utilizat în India încă din secolul al V-lea. Același sistem zecimal pozițional cu semne pentru zero a fost, de asemenea, baza sistemului numeric învățat aproape simultan al astronomilor indieni, în care circumscrierea expresiilor precum „început” (1), „ochi” (2), „cele trei etape temporale” (3) pentru numerele de la 1 la 9 și „cer”, „gol”, „punct” sau alte cuvinte pentru zero au fost clasificate în funcție de zecimalul lor ca o descriere lingvistică a numerelor cu mai multe cifre. Lokavibhaga , scris în Prakrit în 458 , este considerat o dovadă timpurie a unui astfel de cadru pozițional al, în acest caz, al denumirilor lingvistice lingvistice în mare parte nemetaforice , care, cu toate acestea, a supraviețuit doar într-o traducere sanscrită ulterioară. Sistemul numeric circumscriptibil poate fi găsit pe deplin dezvoltat în Bhaskara I (secolul al VII-lea).

Pentru scrierea numerelor, arabii și popoarele arabizate de aceștia au adoptat inițial sistemul aditiv zecimal al numerelor grecești alfabetice, inițial mediat de modelele ebraice și siriene, și au fost transferate la cele 28 de litere ale alfabetului arab. Până cel târziu în secolul al VIII-lea, însă, cifrele indiene și metodele de calcul pe baza acestora au devenit cunoscute mai întâi în Orientul Arab și în cursul secolului al IX-lea în Africa de Nord și Al-Andalus . Cea mai veche mențiune este găsită în secolul al VII-lea de episcopul sirian Severus Sebokht , care laudă în mod expres sistemul indian. Muhammad ibn Musa al-Chwarizmi , care nu numai că a folosit noile cifre în lucrările sale matematice, ci și o introducere, care a fost dată doar în traducerea latină , Kitāb al-Jamʿ în jurul anului 825, a jucat un rol important în răspândirea cuvânt în lumea arabă și occidentală . l-tafrīq bi-ḥisāb al-Hind („Despre aritmetica cu cifre indiene”) cu o descriere a sistemului numeric și a aritmeticii de bază scrise bazate pe acesta, care este potrivită pentru începători .

În 10./11. În secolul al XIX-lea, numerele arabe occidentale sau cifrele derivate din acestea ( numite vârfuri ) au apărut pe pietrele de calcul ale abacului mănăstirii din vestul latin . Cu toate acestea, ele nu au fost folosite dincolo de acestea ca numere sau chiar pentru aritmetica scrisă. Împreună cu abacul mănăstirii, au fost uitați din nou. Al-Chwarizmi a ajutat cifrele indiene să facă o descoperire în adaptările latine și tratatele de limbă populară aferente începând cu secolul al XII-lea. Cuvintele lor inițiale Dixit Algorismi au asigurat că „Algorismul”, redarea latină a numelui său, s-a impus pe scară largă drept numele acestei noi arte a aritmeticii. Mai ales în Italia, în cazul în care Leonardo Fibonacci a făcut cunoscut în lucrarea sa abbaci Liber din propria cunoștințele dobândite în Africa de Nord, calculul numeric indian a fost în măsură să înlocuiască aproape complet abac (cu calcularea pietre) , în finanțe și comerț începând din secolul al 13 - lea Take nume (abbaco) . În alte țări a devenit subiectul instruirii științifice și comerciale, dar până la începutul perioadei moderne a avut un concurent puternic în aritmetică pe linii. Chiar și ca un simplu font de cifră în scopul practic al notării numerelor și al numerotării , pentru care nu este necesar un sistem de valori de poziție, cifrele indo-arabe nu s-au putut afirma treptat decât cu numerele romane încă de la începutul perioadei moderne.

Vezi si

• Numele numerelor

literatură

• John D. Barrow: De ce lumea este matematică / John D. Barrow. Din engleză și cu o postfață de Herbert Mehrtens . Campus-Verl., Frankfurt / Main 1993, ISBN 3-593-34956-6 . 
• Georges Ifrah: Istoria universală a numerelor. Cu filă. Și desen. a autorului. Parkland-Verl., Köln 1998, ISBN 3-88059-956-4 . 
• Karl Menninger: număr și număr. Vol. 2. Script numeric și aritmetică . Vandenhoeck & Ruprecht, 1958. 
• John M. Pullan: Istoria Abacului . Hutchinson, Londra 1968. 

Link-uri web

• Sistem zecimal / zeci pentru școlari explicat pe mathematik-wissen.de
• Înțelegeți sistemul valorii zecimale și învățați să gândiți metacognitiv. Șabloane cu interviuri flexibile, este metoda critică de explorare, Piaget

Dovezi individuale

1. ↑ Harald Haarmann: Istoria mondială a numerelor . Beck, München 2008, ISBN 978-3-406-56250-1 , pp. 29 . 
2. ↑ Urmăriți A051626 în OEIS
3. ↑ Harald Krause, Sabrina Kutscher și altele: cel mai mare bar de tezaur din Europa: Comoara de cupru bronzului timpuriu din Oberding. În: Matthias Wemhoff, Michael M. Rind: Mișcări : arheologie în Germania. Berlin, Petersberg 2018, p. 167 și urm.
4. ↑ J. Stolz: Prima dovadă a sistemului zecimal? Tezaurul de la începutul epocii bronzului de la Oberding. În: Restauro. Jurnal pentru conservare și restaurare , anul 8 2017, pp. 14-19.
5. ↑ Menninger: Număr cuvânt și număr (1958), II, p. 3ff.; Karl-August Wirth, Art. Numere deget. În: Otto Schmidt (Ed.): Reallexikon zur deutschen Kunstgeschichte , Volumul VIII, Metzler Verlag, Stuttgart 1987, Sp. 1229-1310; Ifrah: Istoria universală a numerelor (1998), p. 87.
6. ↑ Menninger: cuvânt de număr și număr (1958), II, p. 104ss.; Ifrah: Universalgeschichte der numbers (1998), p. 136ss.; Pullan, History of the Abacus (1968), pp. 16 și urm.
7. ↑ Menninger: cuvânt și număr număr (1958), p. 131 și urm; Ifrah: Universalgeschichte der numbers (1998), p. 530ff.; Werner Bergmann: Inovații în Quadrivium din secolele X și XI. Studii privind introducerea astrolabului și a abacului în Evul Mediu latin , Steiner Verlag, Stuttgart 1985 (= Sudhoffs Archiv, supliment 26), p. 57ss., P. 174ff.
8. ^ Alfred Nagl: banii aritmetici și aritmetica operațională. În: Jurnalul Numismatic 19 (1887), pp. 309-368; Menninger: număr și număr (1958), II, pp. 140 și urm.; Pullan: History of the Abacus (1968), passim
9. ^ Francis P. Barnard: The Casting Counter and the Counting Board. Un capitol în istoria numismaticii și aritmeticii timpurii , Clarendon Press, Oxford 1916; Menninger: cuvânt de număr și număr (1958), II, p. 152ff., P. 165, p. 178, p. 182f.; Pullan: History of the Abacus (1968), p. 52ss.; Ifrah: Istoria universală a numerelor (1998), p. 146ff.
10. ↑ Ifrah: Universalgeschichte der numbers (1998), p. 411ff., P. 420.
11. ↑ Ifrah: Universalgeschichte der numbers (1998), p. 428ff., P. 511ff.
12. ↑ Ifrah. Istoria universală a numerelor (1998), p. 504 și urm.
13. ↑ Ifrah. Istoria universală a numerelor (1998), p. 486 și urm.
14. ↑ Ifrah: Universalgeschichte der numbers (1998), p. 498ff.
15. ↑ Ifrah: Universalgeschichte der Numbers (1998), p. 493ff.
16. ↑ Ifrah: Istoria universală a numerelor (1998), p. 499f.
17. ↑ Ifrah: Istoria universală a numerelor (1998), p. 307 și urm.
18. ↑ Ifrah: Universalgeschichte der numbers (1998), p. 533ff.