Solid platonic

Cele mai solide platonice (după filozoful grec Platon ) sunt poliedre cu cea mai mare simetrie . Fiecare dintre ele este delimitată de mai mulți poligoane plane congruente ( congruente ) . Un alt nume este corpurile regulate (din latina corpora regularia ).

Există cinci solide platonice. Numele lor conțin numărul exprimat grecesc al suprafețelor lor de delimitare și eder ca o modificare a cuvântului grecesc ἕδρα ( hedra ) (vezi și poliedru ), suprafața germană (seat).

• Tetraedru (cvadruplu, suprafață formată din patru triunghiuri)
• Hexahedron (hexahedron, suprafața a șase pătrate) - a zarurilor
• Octahedron (octaedru, suprafață formată din opt triunghiuri)
• Dodecaedru (dodecaedru, suprafață din doisprezece pentagone) - de asemenea, dodecaedru pentagonal numit pentru a indica suprafața pentagonelor ca fiind specialul său
• Icosaedru (douăzeci de suprafețe, suprafață formată din douăzeci de triunghiuri)

Solidele platonice sunt convexe . Același număr de margini de lungime egală se întâlnesc în fiecare colț al corpului, două suprafețe congruente se întâlnesc la fiecare margine și fiecare suprafață are același număr de colțuri. Deci, nu este posibil să se distingă două colțuri, margini și suprafețe ale corpului unul de altul pe baza relațiilor cu alte puncte ale poliedrului.

Alternativ, solidele platonice pot fi definite ca acele poliedre , pentru care există orice pereche de suprafețe laterale , margini sau colțuri, este întotdeauna o figură de simetrie schimbată între aceste suprafețe, margini sau colțuri. Acest lucru se înțelege cu cea mai mare simetrie posibilă .

Dacă se renunță la indistinguibilitatea suprafețelor și a muchiilor, se vorbește despre solidele arhimedeene . Dacă, pe de altă parte, se renunță la indistinguibilitatea colțurilor și marginilor, se vorbește despre corpurile catalane . Dacă nu se folosește convexitatea, se vorbește despre poliedre regulate și astfel se includ solidele Kepler-Poinsot .

Prezentare generală

Cele cinci solide platonice	Tetraedru	Hexahedron	octaedru	Dodecaedru	Icosaedru
Tipul suprafețelor laterale	triunghiuri echilaterale	Pătrate	triunghiuri echilaterale	pentagoane regulate	triunghiuri echilaterale
Numărul de colțuri / margini ale unei suprafețe	3	Al 4-lea	3	5	3
Numărul de fețe / margini dintr-un colț	3	3	Al 4-lea	3	5
Numărul de colțuri	Al 4-lea	A 8-a	Al 6-lea	20	Al 12-lea
Numărul de margini	Al 6-lea	Al 12-lea	Al 12-lea	30	30
Numărul fețelor	Al 4-lea	Al 6-lea	A 8-a	Al 12-lea	20
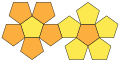
Plasa corpului , fiecare dintre ele prezintă un exemplu din mai multe plase posibile
Numărul de rețele corporale diferite	2	11	11	43380	43380
dual la	Tetraedru	octaedru	Hexahedron	Icosaedru	Dodecaedru
Pictograma Schläfli	{3.3}	{4.3}	{3.4}	{5.3}	{3.5}

proprietăți

O descriere cuprinzătoare a proprietăților solidelor platonice este dată în următoarea listă:

• Suprafața este alcătuită din suprafețe , sunt poliedre .
• Sunt convexe : nu există colțuri sau margini reintrate .
• Toate muchiile au aceeași lungime.
• Toate suprafețele sunt congruente între ele : pot fi convertite una în cealaltă prin rotire și deplasare.
• Toate colțurile au același unghi de suprafață și unghi de margine, toate suprafețele sunt echilaterale și echiangulare .
• Toate colțurile au aceeași distanță de centrul corpului .
• Există o sferă , o sferă de margine și o sferă inc .

Formele colțurilor corpului

Condiția ca numai poligoanele identice să se întâlnească la un colț al corpului este îndeplinită doar de cinci forme de colțuri . Dovada acestui lucru se găsește deja în Euclid . Se bazează pe următoarele considerații:

• Pentru orice colț al corpului, suma unghiurilor interioare ale tuturor suprafețelor alăturate este mai mică de 360 ​​°. Dacă ar fi exact 360 °, suprafețele ar sta într-un singur plan . Chiar și cu mai mult de 360 ​​°, niciun colț nu ar fi posibil.
• Pe de altă parte, cel puțin trei suprafețe trebuie să se întâlnească la fiecare colț al corpului .

Dacă toate suprafețele laterale ale unui corp sunt triunghiuri echilaterale ( unghi interior 60 °), trei, patru sau cinci triunghiuri echilaterale ( suma unghiului 180 °, 240 °, 300 °) se pot întâlni la un colț .

Dacă suprafețele laterale sunt pătrate ( unghi interior 90 °) sau pentagone regulate (unghi interior 108 °), trei dintre ele se pot întâlni ( suma unghiurilor 270 ° pentru pătrate sau 324 ° pentru pentagone).

Suma unghiurilor interioare a 6 triunghiuri echilaterale , 4 pătrate , 4 pentagone regulate sau 3 hexagone regulate este deja 360 ° sau mai mare. Suma de 360 ° a unghiurilor interne ale șase triunghiuri echilaterale, patru pătrate și trei mijloace de hexagoane regulate care nici o zona in spatiul este creat, ci un mod regulat Tigla a planului va avea loc ( a se vedea secțiunea solide platonice decât tilings regulate ale sferei ). Dacă suma unghiurilor interioare este mai mare de 360 ​​°, poligoanele corespunzătoare nu se pot întâlni deloc într-un singur colț comun.

Poligon	Unghiul interior	Poligoane pe colț și colț unghi / poliedru cu astfel de colțuri
		3	Al 4-lea	5	Al 6-lea	≥ 7
Triunghi echilateral	60 °	180 ° / tetraedru	240 ° / octaedru	300 ° / icosaedru	360 °	> 360 °
pătrat	90 °	270 ° / hexaedru	360 °	> 360 °	> 360 °	> 360 °
Pentagon regulat	108 °	324 ° / dodecaedru	> 360 °	> 360 °	> 360 °	> 360 °
Hexagon regulat	120 °	360 °	> 360 °	> 360 °	> 360 °	> 360 °
Șapte sau mai multe colțuri	128,57 grade sau mai mare	> 360 °	> 360 °	> 360 °	> 360 °	> 360 °

dualitate

Pentru fiecare poliedru convex , o cutie poate fi proiectată cu două corpuri . În cazul solidelor platonice, acest lucru se obține prin conectarea punctelor medii ale fețelor laterale adiacente între ele. Corpurile duale în sens restrâns au aceeași sferă de margine . Marginile corespondente ale corpurilor duale se intersectează la unghi drept în punctul în care ating sfera de margine.

Astfel poliedrul dual are atâtea colțuri cât poliedrul de pornire are fețe . Corpul dual are, de asemenea, atâtea suprafețe, cât corpul de pornire are colțuri. Acesta din urmă poate fi imaginat spațial în așa fel încât fiecare suprafață mărită a corpului dual să taie un colț al corpului original. În al treilea rând, poliedrul dual și poliedrul său de pornire au același număr de muchii. Acest lucru poate fi văzut și din construcția de mai sus: Două suprafețe laterale adiacente formează împreună o margine a poliedrului de pornire, iar „conexiunea celor două centre” a acestor suprafețe laterale adiacente reprezintă o margine a corpului dual. De aceea se vorbește a dualității care inversează dimensiunea . Iar inversarea simbolului Schläfli oferă poliedrul dual pentru aceasta.

În cazul solidelor platonice, ca subgrup al poliedrelor convexe , există, de asemenea, următoarele caracteristici speciale în ceea ce privește solidele lor duale : În primul rând, solidele inițiale și duale au aceeași focalizare geometrică . În al doilea rând, câmpul dual al unui câmp platonic este, de asemenea, un câmp platonic în sine. Hexaedrul ( cubul ) și octaedrul , precum și dodecaedrul și icosaedrul formează fiecare o pereche duală . Tetraedrul este dublă în sine, dar dubla tetraedrul este într - o redusă, central simetric poziție, adică adică este „pe dos”. În al treilea rând: dacă repetați construcția de mai sus și construiți corpul dual pentru a forma un corp dual, obțineți un corp inițial redus - adică un corp platonic care poate fi convertit în corpul inițial prin întindere centrică . Ambele au același accent .

• 

  Două tetraedre dual care se întrepătrund, care formează un tetraedru stelar

• 

  Hexaedru ( cub ) și octaedru imbricate , care sunt duale între ele

• 

  Imbricat dodecaedru și icosaedru , care sunt cu dublă între ele

simetrie

Solidele platonice prezintă cea mai mare simetrie posibilă :

• Colțurile, marginile și suprafețele sunt similare, i. Aceasta înseamnă că fiecare colț (margine, suprafață) poate fi mapat pe orice alt colț (margine, suprafață) prin intermediul unei mapări de congruență a corpului.

Ei spun:

• Grupul de simetrie acționează tranzitiv pe colțuri (precum și pe margini și suprafețe).

Se aplică chiar:

• Grupul de simetrie acționează tranzitiv asupra steagurilor . (Un steag este un colț pe o margine pe o suprafață.)

Cele cinci solide platonice sunt deci poliedre regulate . Grupurile de simetrie care apar în ele și subgrupurile lor aparțin grupurilor de puncte discrete . Solidele platonice duale au același grup de simetrie . Aceasta este baza pentru construirea a numeroase alte corpuri, de ex. B. corpul arhimedic . Deci, nu există cinci, ci doar trei dintre aceste grupuri: grupul tetraedric , grupul cub și grupul icosaedric . Acestea joacă un rol în matematică în diferite contexte.

Datorită simetriei lor , modelele fabricate omogen de solide platonice au proprietatea că pot cădea pe fiecare dintre suprafețele lor cu exact aceeași probabilitate atunci când sunt aruncate . Apropo , majoritatea zarurilor nu sunt perfect simetrice din cauza indentărilor pentru numere.

Deltaeder

Deoarece tetraedrul , octaedrul și icosaedrul aparțin, de asemenea , delteedrului convex , un corp din fiecare grup de simetrie aparține deltaedrului.

Bile atingătoare

Din simetria ridicată rezultă imediat: Fiecare solid platonic are

• o sferă inc care atinge toate suprafețele sale și
• o sferă pe care se află toate colțurile sale , precum și
• o sferă de margine pe care se află punctele medii ale marginilor.

Centrul comun al acestor trei sfere este centrul solidului platonic.

Proprietăți matematice

Solidele platonice ca plăci regulate ale sferei

Dacă proiectați marginile unui solid platonic din centru pe o sferă cu același centru, de ex. B. pe sfera înconjurătoare, suprafața sferică este placată cu poligoane sferice regulate, care sunt congruente între ele, cu același număr de margini care se întâlnesc la aceleași unghiuri în fiecare colț. Aceste placări au aceleași simetrii ca și corpul original. În special, acestea sunt, de asemenea , tranzitorii de pavilion . Este vorba despre cele cinci plăci regulate ale sferei, între care există aceleași relații de dualitate ca și între corpuri. Într-un alt context, se vorbește și despre hărți și hărți duale .

Fiecare placă obișnuită poate fi descrisă de o pereche , așa-numitul simbol Schläfli , unde reprezintă numărul de margini ale unui câmp și numărul de margini care se termină într-un colț . Solidele platonice sunt perechile duale ( hexaedru ) și ( octaedru ), ( dodecaedru ) și ( icosaedru ), precum și autodualitatea ( tetraedru ). ${\ displaystyle \ {p, q \}}$${\ displaystyle p}$${\ displaystyle q}$ ${\ displaystyle \ {4,3 \}}$${\ displaystyle \ {3,4 \}}$${\ displaystyle \ {5.3 \}}$${\ displaystyle \ {3.5 \}}$${\ displaystyle \ {3,3 \}}$

Geometric, aceasta înseamnă pentru solidele platonice care

• ${\ displaystyle p}$este numărul de colțuri ale celor fețele laterale . Prin urmare, fețele laterale ale solidului platonic sunt colțuri regulate .${\ displaystyle p}$
• ${\ displaystyle q}$sunt numărul de fețe / margini ale solidului platonic care se întâlnesc la un colț.

Suma unghiurilor interioare dintr-un colț al solidului platonic este deci (vezi Poligon regulat - unghi ). Acest lucru are ca rezultat inegalitatea${\ displaystyle q \ cdot {\ tfrac {p-2} {p}} \ cdot 180 ^ {\ circ}}$

${\ displaystyle {\ begin {align} q \ cdot {\ tfrac {p-2} {p}} \ cdot 180 ^ {\ circ} & <360 ^ {\ circ} \ Rightarrow \\ {\ frac {1} {p}} + {\ frac {1} {q}} &> {\ frac {1} {2}} \ left (p, q \ in \ mathbb {N} \ right) \ end {align}}}$

cu soluțiile de mai sus . Această relație rezultă, de asemenea, din teorema lui Euler a poliedrelor , care leagă numărul de colțuri, margini și suprafețe unul cu celălalt: ${\ displaystyle E}$${\ displaystyle K}$${\ displaystyle F}$

${\ displaystyle E-K + F = 2}$,

unde constanta 2 este caracteristică sferei .

În geometria euclidiană se aplică graficelor plane infinit de mari, cu o interpretare adecvată și anume asimptotică a ecuației

${\ displaystyle E-K + F = 0}$

sau

${\ displaystyle {\ frac {1} {p}} + {\ frac {1} {q}} = {\ frac {1} {2}} \ left (p, q \ in \ mathbb {N} \ right )}}$

cu soluțiile

${\ displaystyle \ {4,4 \}}$(auto- dual ), precum și și dual la acesta , care reprezintă cele trei plăci platonice ale planului (prin pătrate , triunghiuri echilaterale și hexagone regulate ), care reprezintă generalizări ale solidelor platonice.${\ displaystyle \ {3,6 \}}$${\ displaystyle \ {6.3 \}}$

Cele Soluțiile din

${\ displaystyle {\ frac {1} {p}} + {\ frac {1} {q}} <{\ frac {1} {2}} \ (p, q \ in \ mathbb {N})}$

asigură placarea regulată a geometriei hiperbolice .

Pentru solidele platonice nu este doar adevărat , ci și . Acest sistem exclusiv întreg de ecuații alcătuit din trei ecuații poate fi rezolvat și are ca rezultat numărul de colțuri, margini și suprafețe: ${\ displaystyle E-K + F = 2}$${\ displaystyle p \ times E = 2 \ times K = q \ times F}$ ${\ displaystyle E}$${\ displaystyle K}$${\ displaystyle F}$

${\ displaystyle E = {\ frac {4 \ cdot p} {4- (p-2) \ cdot (q-2)}}}$

${\ displaystyle K = {\ frac {2 \ cdot p \ cdot q} {4- (p-2) \ cdot (q-2)}}}$

${\ displaystyle F = {\ frac {4 \ cdot q} {4- (p-2) \ cdot (q-2)}}}$

Pentru fiecare solid platonic, numărul de colțuri, margini și suprafețe poate fi calculat numai prin specificarea și (vezi mai sus), fără a cunoaște proprietățile geometrice exacte . ${\ displaystyle p}$${\ displaystyle q}$

Prezentare generală

Considerente Generale solidele platonice	Caz general	Tetraedru	Hexahedron	octaedru	Dodecaedru	Icosaedru
Pictograma Schläfli	${\ displaystyle \ {p, q \}}$	{3.3}	{4.3}	{3.4}	{5.3}	{3.5}
Numărul de colțuri	${\ displaystyle E = {\ frac {4 \ cdot p} {4- (p-2) \ cdot (q-2)}}}$	Al 4-lea	A 8-a	Al 6-lea	20	Al 12-lea
Numărul de margini	${\ displaystyle K = {\ frac {2 \ cdot p \ cdot q} {4- (p-2) \ cdot (q-2)}}}$	Al 6-lea	Al 12-lea	Al 12-lea	30	30
Numărul fețelor	${\ displaystyle F = {\ frac {4 \ cdot q} {4- (p-2) \ cdot (q-2)}}}$	Al 4-lea	Al 6-lea	A 8-a	Al 12-lea	20
Unghiurile interioare ale suprafețelor laterale	${\ displaystyle \ alpha = {\ tfrac {p-2} {p}} \ cdot 180 ^ {\ circ}}$	60 °	90 °	60 °	108 °	60 °
Suma unghiurilor interioare	${\ displaystyle q \ cdot {\ tfrac {p-2} {p}} \ cdot 180 ^ {\ circ}}$	180 °	270 °	240 °	324 °	300 °
Defect unghiular (360 ° - suma unghiurilor interioare )	${\ displaystyle (2-q \ cdot {\ tfrac {p-2} {p}}) \ cdot 180 ^ {\ circ}}$	180 °	90 °	120 °	36 °	60 °

Suprafață

Pentru aria suprafața , lungimea laturii solide platonice și Schläfli simbolul aplică${\ displaystyle a}$${\ displaystyle \ {p, q \}}$

${\ displaystyle A_ {O} = {\ frac {p \ cdot q \ cdot a ^ {2}} {4- (p-2) \ cdot (q-2)}} \ cdot \ cot \ left ({\ frac {\ pi} {p}} \ right)}$

deoarece suprafața este compus din congruente regulate - colturi ( a se vedea Regular Poligon - zona de dimensiune și de suprafață ) ${\ displaystyle F = {\ tfrac {4 \ cdot q} {4- (p-2) \ cdot (q-2)}}}$ ${\ displaystyle p}$

Unghiul dintre fețele adiacente

Următoarele se aplică unghiul dintre adiacente suprafețe ( unghiul diedru ) ${\ displaystyle \ beta}$

${\ displaystyle \ beta = 2 \ cdot \ arcsin \ left ({\ frac {\ cos \ left ({\ frac {\ pi} {q}} \ right)} {\ sin \ left ({\ frac {\ pi } {p}} \ right)}} \ right) \ Leftrightarrow \ sin \ left ({\ frac {\ beta} {2}} \ right) = {\ frac {\ cos \ left ({\ frac {\ pi } {q}} \ right)} {\ sin \ left ({\ frac {\ pi} {p}} \ right)}}}$

din cauza , deoarece solidele platonice sunt convexe. ${\ displaystyle 0 <\ beta <\ pi}$

Pentru aceasta este suficient să se ia în considerare o diagonală (vezi poligon regulat - diagonalele ) a regulate - colț , care este întins ca o umbrelă de colțurile marginilor care se întâlnesc la un anumit colț de , iar cele două la fel de lungi înălțimi de la sfârșitul punctele (colțurile) acestei diagonale la marginea care leagă colțul luat în considerare cu colțul sărit peste diagonală . Pe acest triunghi isoscel se poate aplica sinusul . ${\ displaystyle d_ {2}}$ ${\ displaystyle q}$${\ displaystyle d_ {2}}$

Laturile acestui regulat - gon ( „Umbrela“), a diagonalelor de suprafețele laterale ale solid platonic, adică regulat -Ecke lungimea laterală a, care se întâlnesc la colțul relevant. Ai lungimea ${\ displaystyle q}$ ${\ displaystyle d_ {2}}$${\ displaystyle p}$

${\ displaystyle {\ frac {a \ cdot \ sin \ left ({\ frac {2 \ cdot \ pi} {q}} \ right)} {\ sin \ left ({\ frac {\ pi} {q}} \ right)}} = 2 \ cdot a \ cdot \ cos \ left ({\ frac {\ pi} {q}} \ right)}$

Umkugelradius, raza mingii de margine, incugelradius

Din acest unghi între adiacente suprafețele eboșei Umkugelradius , raza marginii sferei și Inkugelradius de Platonic solide determină prin adăugarea circumscris și Inkreisradius afectat suprafața laterală , un mod regulat - Eck este considerat ( a se vedea Regular Poligon - cerc ca formă de delimitare ): ${\ displaystyle \ beta}$ ${\ displaystyle r_ {u}}$ ${\ displaystyle r_ {k}}$ ${\ displaystyle r_ {i}}$ ${\ displaystyle p}$

${\ displaystyle r_ {u} = {\ frac {a} {2}} \ cdot \ tan \ left ({\ frac {\ pi} {q}} \ right) \ cdot \ tan \ left ({\ frac { \ beta} {2}} \ right)}$

${\ displaystyle r_ {k} = {\ frac {a} {2}} \ cdot {\ frac {\ cos \ left ({\ frac {\ pi} {p}} \ right)} {\ cos \ left ( {\ frac {\ pi} {q}} \ right)}} \ cdot \ tan \ left ({\ frac {\ beta} {2}} \ right)}$

${\ displaystyle r_ {i} = {\ frac {a} {2}} \ cdot \ cot \ left ({\ frac {\ pi} {p}} \ right) \ cdot \ tan \ left ({\ frac { \ beta} {2}} \ right)}$

Unghiuri solide în colțuri

În 2015, HC Rajpoot a publicat o formulă simplă pentru unghiul solid al colțului

${\ displaystyle \ Omega = 2 \ pi -2n \ cdot \ arcsin \ left (\ cos \ left ({\ frac {\ pi} {n}} \ right) \ cdot {\ sqrt {\ tan ^ {2} \ left ({\ frac {\ pi} {n}} \ right) - \ tan ^ {2} \ left ({\ frac {\ alpha} {2}} \ right)}} \ right),}$

care este utilizat în toate cele cinci solide platonice. Aici cele două variabile medii

• ${\ displaystyle n}$ numărul de margini / suprafețe care se întâlnesc la un colț al solidului platonic, adică pentru

	Tetraedru, cub și dodecaedru	${\ displaystyle n = 3}$ ,
	octaedru	${\ displaystyle n = 4}$ si pentru
	Icosaedru	${\ displaystyle n = 5}$ ;

• iar unghiul interior al unei suprafețe a câmpului platonic, adică pentru${\ displaystyle \ alpha}$

	Tetraedru, octaedru și icosaedru	${\ displaystyle \ alpha = 60 ^ {\ circ} = \ pi / 3}$ ,
	cub	${\ displaystyle \ alpha = 90 ^ {\ circ} = \ pi / 2}$ si pentru
	Dodecaedru	${\ displaystyle \ alpha = 108 ^ {\ circ} = 3 \ pi / 5}$ .

volum

Din suprafață și din volum rezultând Inkugelradius , deoarece fiecare solid platonic poate fi împărțit în piramide obișnuite descompune suprafața laterală , atât de regulată - Eck , ca bază și Inkugelradius ca înălțime au: ${\ displaystyle F = {\ tfrac {4 \ cdot q} {4- (p-2) \ cdot (q-2)}}}$ ${\ displaystyle p}$

${\ displaystyle {\ begin {align} V & = {\ frac {1} {3}} \ cdot A \ cdot r_ {i} = {\ frac {1} {3}} \ cdot {\ frac {p \ cdot q \ cdot a ^ {2}} {4- (p-2) \ cdot (q-2)}} \ cdot \ cot \ left ({\ frac {\ pi} {p}} \ right) \ cdot {\ frac {a} {2}} \ cdot \ cot \ left ({\ frac {\ pi} {p}} \ right) \ cdot \ tan \ left ({\ frac {\ beta} {2}} \ dreapta) \\ & = {\ frac {p \ cdot q \ cdot a ^ {3}} {24-6 \ cdot (p-2) \ cdot (q-2)}} \ cdot \ cot ^ {2} \ left ({\ frac {\ pi} {p}} \ right) \ cdot \ tan \ left ({\ frac {\ beta} {2}} \ right) \ end {align}}}$

Formule

Dimensiunile unui câmp platonic cu p colțuri / margini pe suprafață, q suprafețe / margini într-un colț și lungimea muchiei a
	Caz general	Exemplu de dodecaedru
Pictograma Schläfli	${\ displaystyle \ {p, q \}}$	${\ displaystyle \ {5.3 \}}$
volum	${\ displaystyle V = {\ frac {p \ cdot q \ cdot a ^ {3}} {24-6 \ cdot (p-2) \ cdot (q-2)}} \ cdot \ cot ^ {2} \ left ({\ frac {\ pi} {p}} \ right) \ cdot \ tan \ left ({\ frac {\ beta} {2}} \ right)}$	${\ displaystyle V \ approx 7 {,} 663 \ cdot a ^ {3}}$
Suprafață	${\ displaystyle A_ {O} = {\ frac {p \ cdot q \ cdot a ^ {2}} {4- (p-2) \ cdot (q-2)}} \ cdot \ cot \ left ({\ frac {\ pi} {p}} \ right)}$	${\ displaystyle A_ {O} \ approx 20 {,} 646 \ cdot a ^ {2}}$
Umkugelradius	${\ displaystyle r_ {u} = {\ frac {a} {2}} \ cdot \ tan \ left ({\ frac {\ pi} {q}} \ right) \ cdot \ tan \ left ({\ frac { \ beta} {2}} \ right)}$	${\ displaystyle r_ {u} \ approx 1 {,} 401 \ cdot a}$
Raza mingii de margine	${\ displaystyle r_ {k} = {\ frac {a} {2}} \ cdot {\ frac {\ cos \ left ({\ frac {\ pi} {p}} \ right)} {\ cos \ left ( {\ frac {\ pi} {q}} \ right)}} \ cdot \ tan \ left ({\ frac {\ beta} {2}} \ right)}$	${\ displaystyle r_ {k} \ approx 1 {,} 309 \ cdot a}$
Inc raza sferei	${\ displaystyle r_ {i} = {\ frac {a} {2}} \ cdot \ cot \ left ({\ frac {\ pi} {p}} \ right) \ cdot \ tan \ left ({\ frac { \ beta} {2}} \ right)}$	${\ displaystyle r_ {i} \ approx 1 {,} 114 \ cdot a}$
Raportul razei sferei la raza sferei	${\ displaystyle {\ frac {r_ {i}} {r_ {u}}} = \ cot \ left ({\ frac {\ pi} {p}} \ right) \ cdot \ cot \ left ({\ frac { \ pi} {q}} \ right)}$	${\ displaystyle {\ frac {r_ {i}} {r_ {u}}} \ approx 0 {,} 795}$
Raportul volumului la volum sferic	${\ displaystyle {\ frac {V} {V_ {UK}}} = {\ frac {1} {\ pi}} \ cdot {\ frac {p \ cdot q \ cdot a ^ {3}} {4- ( p-2) \ cdot (q-2)}} \ cdot \ cot ^ {2} \ left ({\ frac {\ pi} {p}} \ right) \ cdot \ cot ^ {3} \ left ({ \ frac {\ pi} {q}} \ right) \ cdot \ cot ^ {2} \ left ({\ frac {\ beta} {2}} \ right)}$	${\ displaystyle {\ frac {V} {V_ {UK}}} \ approx 0 {,} 665}$
Raportul volumului sferic la volum	${\ displaystyle {\ frac {V_ {IK}} {V}} = \ pi \ cdot {\ frac {4- (p-2) \ cdot (q-2)} {p \ cdot q \ cdot a ^ { 3}}} \ cdot \ cot \ left ({\ frac {\ pi} {p}} \ right) \ cdot \ tan ^ {2} \ left ({\ frac {\ beta} {2}} \ right) }$	${\ displaystyle {\ frac {V_ {IK}} {V}} \ approx 0 {,} 755}$
Unghiul interior al suprafeței laterale ( regulat - colț )${\ displaystyle p}$	${\ displaystyle \ left (1 - {\ frac {2} {q}} \ right) \ cdot 180 ^ {\ circ}}$	${\ displaystyle \ alpha = 108 ^ {\ circ}}$
Unghiul dintre fețele adiacente	${\ displaystyle \ beta = 2 \ cdot \ arcsin \ left ({\ frac {\ cos \ left ({\ frac {\ pi} {q}} \ right)} {\ sin \ left ({\ frac {\ pi } {p}} \ right)}} \ right)}$	${\ displaystyle \ beta \ approx 116 ^ {\ circ} \; 33 ^ {\ prime} \; 54 ^ {\ prime \ prime}}$
Unghiuri solide în colțuri	${\ displaystyle \ Omega = 2 \ cdot \ pi -2 \ cdot p \ cdot \ arcsin \ left (\ cos \ left ({\ frac {\ pi} {p}} \ right) \ cdot {\ sqrt {\ tan ^ {2} \ left ({\ frac {\ pi} {p}} \ right) - \ tan ^ {2} \ left (\ left ({\ frac {1} {2}} - {\ frac {1 } {q}} \ right) \ cdot \ pi \ right)}} \ right)}$	${\ displaystyle \ Omega \ approx 2 {,} 962 \; \ mathrm {sr}}$

Notă: Următoarele se aplică unghiul dintre adiacente suprafețe ( unghi diedru ) ( a se vedea arctangentă și arctangentă ): ${\ displaystyle \ beta}$

${\ displaystyle \ tan \ left ({\ frac {\ beta} {2}} \ right) = \ tan \ left (\ arcsin \ left ({\ frac {\ cos \ left ({\ frac {\ pi} { q}} \ right)} {\ sin \ left ({\ frac {\ pi} {p}} \ right)}} \ right) \ right) = \ left ({\ frac {\ sin ^ {2} \ left ({\ frac {\ pi} {p}} \ right)} {\ cos ^ {2} \ left ({\ frac {\ pi} {q}} \ right)}} - 1 \ right) ^ { - {\ frac {1} {2}}}}$din cauza și${\ displaystyle \ tan (\ arcsin (x)) = {\ frac {x} {\ sqrt {1-x ^ {2}}}}}$

${\ displaystyle \ cot \ left ({\ frac {\ beta} {2}} \ right) = \ cot \ left (\ arcsin \ left ({\ frac {\ cos \ left ({\ frac {\ pi} { q}} \ right)} {\ sin \ left ({\ frac {\ pi} {p}} \ right)}} \ right) \ right) = \ left ({\ frac {\ sin ^ {2} \ left ({\ frac {\ pi} {p}} \ right)} {\ cos ^ {2} \ left ({\ frac {\ pi} {q}} \ right)}} - 1 \ right) ^ { \ frac {1} {2}}}$din cauza .${\ displaystyle \ cot (\ arcsin (x)) = {\ frac {\ sqrt {1-x ^ {2}}} {x}}}$

Solidele platonice din solidele platonice

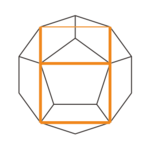
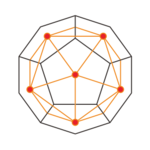
Un solid platonic poate fi descrisă ca fiind înscrisă într - un alt solid platonic dacă toate sale colțuri ating pe suprafețele laterale ale solidului exterior. În schema următoare există și câteva cazuri interesante în care nu toate colțurile sunt pe fețele laterale. Pe lângă colțuri, figurile arată și marginile și suprafețele care ating corpul exterior. Numărul lor este indicat mai jos.

	Tetraedru	Hexahedron	octaedru	Dodecaedru	Icosaedru
Tetraedru
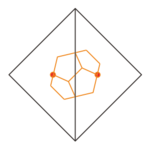
	toate cele 4 colțuri	toate cele 8 colțuri 4 din 12 margini	toate cele 6 colțuri la fiecare 12 margini 4 din 8 suprafețe	4 din 20 de colțuri	toate cele 12 colțuri 12 din 30 de margini 4 din 20 de zone
Hexahedron
	toate cele 4 colțuri toate cele 6 margini		toate cele 6 colțuri	12 din 20 de colțuri 6 din 30 de margini	toate cele 12 colțuri 6 din 30 de margini
octaedru
	toate cele 4 colțuri	toate cele 8 colțuri		8 din 20 de colțuri	toate cele 12 colțuri 24 din 30 de margini 8 din 20 de spații
Dodecaedru
	toate cele 4 colțuri	toate cele 8 colțuri la fiecare 12 margini	toate cele 6 colțuri		toate cele 12 colțuri
Icosaedru
	toate cele 4 colțuri	toate cele 8 colțuri	toate cele 6 colțuri	la fiecare 20 de colțuri

Grafic proprietăți teoretice

Toate graficele solidelor platonice sunt grafice regulate, deoarece același număr de muchii se întâlnesc la fiecare colț al acestor poliedre . Cel mai scurt ciclu , așa-numita dimensiune a taliei , este egal cu numărul de colțuri ale fețelor laterale ale solidului platonic în cauză.

The-graph teoretic diametrul și-grafic teoretic raza de acord , deoarece toate nodurile sunt grafic teoretic echivalente una cu alta și pot fi mapate împreună cu graficul pe un grafic izomorf cu ajutorul permutări . Rezultă că toate nodurile au aceeași excentricitate și aparțin atât marginii, cât și centrului graficului.

Rețele

Ca toate poliedrele, solidele platonice au rețele diferite (a se vedea prezentarea de mai sus). Există diferite moduri de a desfășura un poliedru gol prin tăierea unor margini și extinderea acestuia în plan . Dacă numărul muchiilor și numărul fețelor poliedrului sunt, atunci se creează o plasă a corpului prin tăierea marginilor. În colțuri sunt în mod evident pe marginea plasei. Celelalte margini conectează poligoanele obișnuite ale rețelei. ${\ displaystyle K}$${\ displaystyle F}$${\ displaystyle K-F + 1}$${\ displaystyle F-1}$

Fiecare solid platonic, ca orice poliedru convex , are atribuit un grafic plan nedirecționat . Acest grafic este regulat , datorită marginilor care merg la fiecare nod , astfel încât gradul pentru toate nodurile este egal , unde numărul de noduri. Gradul de nod este egal cu numărul de fețe (și margini ) , care se întâlnesc în fiecare colț al solid platonic. În cazul graficelor plane, dispunerea geometrică exactă a nodurilor nu este importantă. Cu toate acestea, este important ca marginile să nu se intersecteze. Nodurile acestui grafic corespund colțurilor poliedrului. ${\ displaystyle {\ tfrac {2 \ cdot K} {E}}}$${\ displaystyle {\ tfrac {2 \ cdot K} {E}}}$${\ displaystyle E}$

Cele tăiate marginile fiecărei rețele , împreună cu colțuri ( nodurile ) formează un arbore de acoperire al graficului. Fiecare rețea corespunde exact unui copac care se întinde și invers, astfel încât să existe o atribuire unu-la-unu ( bijectiv ) între rețele și copaci care se întind. Dacă considerați o rețea de corp fără zona exterioară ca un grafic, obțineți un grafic dual fiecare cu un arbore cu noduri și margini și gradul maxim de nod . Fiecare zonă a solidului platonic este alocată unui nod al arborelui. ${\ displaystyle K-F + 1}$${\ displaystyle F}$${\ displaystyle F-1}$ ${\ displaystyle {\ tfrac {2 \ cdot K} {F}}}$

Aceste considerații sunt legate de substituția poliedrului Euler .

Grafice și culori duale

Numărul minim de culori care este necesar pentru a colora nodurile unui grafic în așa fel încât nodurile învecinate să fie întotdeauna colorate diferit se numește numărul cromatic (vezi colorarea nodului ). Numărul corespunzător pentru margini se numește index cromatic (vezi colorarea marginilor ). În cazul graficelor solidelor platonice, acesta este egal cu gradul (maxim) al nodului. În legătură cu teorema lui Vizing , acestea se numesc grafuri de clasa 1 .

În nodurile icosahedral Graficul poate fi colorat cu 4 culori , astfel încât nodurile învecinate sunt întotdeauna colorate diferit. Aceasta înseamnă că numărul cromatic al acestui grafic este 4 (vezi colorarea nodului ). În plus, marginile pot fi colorate cu 3 culori, astfel încât marginile adiacente să fie întotdeauna colorate diferit. Acest lucru nu este posibil cu 2 culori, deci indicele cromatic pentru colorarea marginilor este de 3.

Graficul dublu este util în determinarea numărului necesar de culori pentru zone sau zone . Acest concept teoretic grafic al dualității este într-o anumită măsură o analogie sau o generalizare a dualității geometrice a poliedrelor (vezi secțiunea de mai sus ).

Nodurile acestui grafic dual sunt atribuite unu-la-unu (bijectiv) zonelor grafului original și invers (vezi funcția bijectiv ). Pentru graficul dodecaedru (a se vedea figurile), de exemplu, se aplică următoarele: Nodurile grafului dual icosaedru pot fi colorate cu 4 culori, astfel încât nodurile vecine să fie întotdeauna colorate diferit, dar nu cu 3 culori, astfel încât numărul cromatic de graficul icosaedru este 4. Din aceasta se poate concluziona indirect: Deoarece numărul cromatic este de 4, sunt necesare 4 culori pentru o astfel de colorare a suprafeței dodecaedrului sau o colorare a zonelor grafului dodecaedrului.

Cercurile Hamilton

Toate graficele solidelor platonice au mai multe cercuri Hamilton . Aceasta este o cale închisă într-un grafic care conține fiecare nod exact o dată. În cazul cubului și al dodecaedrului , acest lucru este totul în afară de evident. Este clar pentru tetraedrul asociat graficului complet . Pentru octaedru, existența cercurilor Hamilton rezultă dintr-o teoremă de Gabriel Andrew Dirac , pentru icosaedrul dintr-o teoremă de William Thomas Tutte (vezi teoremele despre cercurile Hamilton ). ${\ displaystyle K_ {4}}$

Cu toate acestea , nu există o formulă matematică și nici un algoritm cu adevărat simplu pentru numărul de cercuri Hamilton . Investigațiile cu computerul arată, de exemplu, că icosaedrul are 2560 de cercuri Hamilton.

Cercuri Euler

În graficele de tetraedru , cub , dodecaedru și icosaedru nu au cercuri Euler , deoarece gradele de toate nodurile sunt ciudat. Acest lucru se datorează faptului că un număr impar de muchii se întâlnesc în fiecare colț al acestor poliedre . Octoedrul are 1844 cercuri Euler, deoarece studiile efectuate cu calculatorul spectacol.

Prezentare generală

Cele cinci solide platonice	Tetraedru	Hexahedron	octaedru	Dodecaedru	Icosaedru
poliedru
grafic regulat asociat
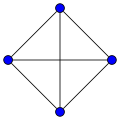
număr cromatic (vezi colorarea nodului )	Al 4-lea	2	3	3	Al 4-lea
index cromatic (vezi colorarea muchiilor )	3	3	Al 4-lea	3	5
Număr pentru colorarea suprafeței (vezi graficul dual )	Al 4-lea	3	2	Al 4-lea	3
Gradul nodului (vezi graficul regulat )	3	3	Al 4-lea	3	5
Numărul conexiunii nodului	3	3	Al 4-lea	3	5
Numărul conexiunii marginale	3	3	Al 4-lea	3	5
cel mai scurt ciclu ( dimensiunea taliei )	3	Al 4-lea	3	5	3
grafic diametrul teoretic	1	3	2	5	3
raza grafic-teoretică	1	3	2	5	3
Numărul de clici	Al 4-lea	2	3	2	3
Numărul de stabilitate	1	Al 4-lea	2	A 8-a	3
Numărul cercurilor Hamilton	Al 6-lea	Al 12-lea	32	60	2560
Numărul de cercuri Euler	0	0	1488	0	0

Poliedre derivate din solidele platonice

Datorită regularității puternice a solidelor platonice, este ușor să se obțină alte solide din ele, care sunt din nou foarte regulate. Trebuie doar să utilizați aceleași construcții simetric pe suprafețe , margini sau colțuri . Un exemplu în acest sens sunt corpurile duale care rezultă din conectarea centrului fiecărei suprafețe cu centrele suprafețelor adiacente.

Solidele platonice trunchiate

Dacă creați un poliedru trunchiat pornind de la un solid platonic tăind colțurile acestuia astfel încât toate muchiile să aibă aceeași lungime, obțineți un solid arhimedian . Acest corp este, de asemenea, creat ca o secțiune a corpului platonic cu corpul său dual mărit corespunzător .

• 

  Tetraedru trunchiat

• 

  Hexaedru trunchiat

• 

  Otaedru trunchiat

• 

  Dodecaedru trunchiat

• 

  Icosaedru trunchiat (corp de fotbal)

Solidele arhimediene sunt exemple de solide destul de regulate care utilizează poligoane care sunt regulate, dar cu un număr diferit de laturi.

Corpul stelei

Dacă construiți piramide pe suprafețele laterale în loc să le tăiați, veți obține corpuri stelare precum tetraedrul stelar .

Dacă se utilizează triunghiuri echilaterale pentru piramide , există exemple de poliedre care constau în întregime din aceleași poligoane , dar în care numere diferite se ciocnesc în colțuri .

generalizare

Matematicianul elvețian Ludwig Schläfli a determinat rudele- dimensionale ale solidelor platonice în 1852 - dar opera sa a rămas neobservată mult timp. S-a dovedit că în spațiul cu patru dimensiuni există un echivalent în patru dimensiuni, un 4-politop regulat , la fiecare dintre cele cinci corpuri tridimensionale regulate (3-politopi) : la tetraedru celula 5 ( pentacoron ), la cub 8 celule ( Tesseract ), pentru octaedru 16 celule (Hexadekachor), pentru dodecaedru 120 celule ( Hekatonikosachor ) și pentru icosaedru 600 celule ( Hexakosichor ). Apoi, există un al șaselea 4-politop obișnuit: celula 24 (Ikositetrachor).${\ displaystyle n}$

În spațiul cu cinci dimensiuni - și, de asemenea, în toate încăperile de dimensiuni superioare - există în loc de cinci sau șase doar trei politopi obișnuiți: ca Simplex , hiper tetraedrul , ca Maßpolytop , hipercubul și politopul încrucișat , dualul său, Hyperoktaeder .

istorie

Solidele platonice au fost studiate din cele mai vechi timpuri . The Pitagoreicii (secolul 6 BC) distinge cel puțin între tetraedru, hexaedru și dodecaedru. Este posibil ca octaedrul să fi fost ignorat deoarece a fost privit ca o piramidă dublă. Atenienii Theaitetos (415-369 v. Chr.) De asemenea , cunoscut octaedru și icosaedru. El a dovedit că pot exista doar cinci poliedre regulate convexe.

Filosoful grec Platon (aprox. 427–347 î.Hr.), un contemporan al lui Theaetetus, a fost omonimul celor cinci corpuri. În lucrarea sa Timeu (cap. 20, 53c4–55c6) le-a descris în detaliu. El a încorporat solidele platonice în sistemul său filosofic atribuindu-le (cu excepția dodecaedrului) celor patru elemente (cap. 21, 55c7–56c7): focul a reprezentat tetraedrul, aerul pentru octaedru. Icosaedrul era asociat cu apa , hexaedrul cu pământul . Conform acestei teorii, dodecaedrul ar putea fi echivalat cu cel de -al cincilea element, eterul, postulat de Aristotel .

Euclid (360-280 î.Hr.) a descris solidele platonice în XIII. Cartea elementelor sale (§§ 13-17). În el a demonstrat, printre altele, că sunt exact cinci (§ 18a). Hypsikles a preluat „XIV. Cartea ”(din secolul al II-lea î.Hr.) a făcut câteva calcule de volum. „XV. Cartea ”(din secolul al VI-lea d.Hr.) conținea descoperiri suplimentare de către matematicieni greci cu privire la cele cinci solide obișnuite.

Odată cu apariția perspectivei , mai mulți artiști au prelucrat solidele platonice în lucrările lor: Piero della Francesca , Leonardo da Vinci (ilustrații pentru Divina Proportione de Luca Pacioli ), Albrecht Dürer , Wenzel Jamnitzer ( Perspectiva Corporum Regularium , 1568).

Johannes Kepler a reușit ( Mysterium Cosmographicum , 1596) să descrie razele orbitale ale celor șase planete cunoscute la acea vreme folosind o secvență specifică a celor cinci corpuri și a sferelor lor interioare și exterioare. Această interpretare a fost în mare parte de acord cu valorile astronomice cunoscute la acea vreme, dar de fapt nu corespundea nicio regularitate.

Aplicații

Regularitatea izbitoare face ca solidele platonice să fie interesante pentru oameni în multe feluri.

• Unele solide platonice sunt soluții la problema lui Thomson (după Joseph John Thomson ): În termeni grafici, această problemă descrie modul în care n electroni sunt distribuiți pe o suprafață sferică, astfel încât energia potențială prin câmpul lor electric este minimă.
• În plus față de cubul clasic, geometric, ușor de fabricat și folosit de jocuri de noroc de mii de ani , celelalte solide platonice (cunoscute și sub numele de zaruri) sunt folosite astăzi în joc, de ex. B. în jocurile de rol cu ​​stilou și hârtie (vezi zarurile ). Condițiile preliminare pentru aceasta sunt o distribuție densă uniformă din punct de vedere fizic - adică material omogen - precum și proprietățile similare ale tuturor colțurilor și marginilor.
• Solidele platonice au fost mult timp obiecte ale artiștilor vizuali . În arta modernă , MC Escher, în special, s-a ocupat de ele și de corpuri regulate similare acestora; Lucrările lui Salvador Dalí abordează, de asemenea, solidele platonice sau dezvoltarea acestora.
• Poliedrele platonice joacă, de asemenea, un rol important în jocul de aventură The Dig .

• Scopul dodecaedrului pentagonului roman este încă speculat astăzi.
• Rudolf von Laban și-a concretizat teoria mișcării ritmice de cameră (coregrafie) în principal în modelul icosaedrului.
• În gestionarea echipelor, conform unei sugestii a Stafford Beer , solidele platonice pot fi utilizate ca model pentru rețea atunci când angajații se concentrează pe subiectele lor. Fiecare angajat corespunde unei margini, fiecare subiect unui colț al unui solid platonic. Pentru fiecare subiect, vă întâlniți în mod regulat cu toți angajații ale căror margini converg în acest colț de subiecte. Un angajat lucrează la maximum două subiecte în același timp și se poate concentra bine. Chiar și cu echipe mari (de exemplu, icosahedron = 30 de angajați, 5 angajați pe subiect, 12 subiecte), acest lucru asigură existența ordinii. Ideea lui Beer a fost preluată la Centrul de Management din Sankt Gallen și a fost propusă o metodă bazată pe acesta numită Syntegrity .

Chiar și în natură, regularitățile existente pot fi exprimate ca solide platonice.

• Aranjamentul atomilor de hidrogen, de exemplu în orbitalul metan hibrid sp³-hibridizat , corespunde unui tetraedru.
• Tetraedrele, cuburile și octaedrele apar în natură ca cristale (idealizate) ; elementele de simetrie dodecaedrică și icosaedrică se găsesc în cvasicristale .
• Dodecaedrele exacte nu apar ca cristale. Cristale ale anumitor minerale, cum ar fi B. Pirita , care arată ca un dodecaedru din exterior, nu este exact dodecaedru pentagonal , ci mai degrabă distorsionat. Cu toate acestea, distorsiunea este adesea invizibilă cu ochiul liber de la distanță. Cu toate acestea, dacă priviți de aproape, puteți vedea că aceste corpuri nu sunt formate din pentagone regulate (dar neregulate). De exemplu, clorura de sodiu și alumul , care este dopat cu anumite alte substanțe atunci când sunt precipitate, formează cristale cub. Alunul pur cristalizează sub forma unui octaedru. Delimitarea dintre formele individuale nu este absolută, dar simetria internă poate fi exprimată în moduri diferite. În mineralogie, toate solidele platonice tetraedru, cub și octaedru precum și dodecaedru rombic , cuboctaedru și formele lor mixte se încadrează sub termenul cubic . Câteva minerale pot presupune în consecință mai multe dintre aceste forme cubice. Aceasta include, de exemplu, pirita, care apare atât ca un cub, cât și ca un octaedru sau, așa cum a fost descris mai sus, ca un dodecaedru distorsionat.
• Solidele platonice, în special icosaedrul , sunt foarte des forme structurale, deoarece sunt observate în grupuri (adică nanoparticule mici).
• Unele dintre solidele platonice sunt alcătuite din molecule de hidrocarburi organice (vezi hidrocarburi platonice ).
• Dodecaedrul este cea mai mică formă posibilă a moleculelor de carbon goale cunoscute sub numele de fullereni .
• Capsidele proteice ale virușilor pot avea forme diferite, de exemplu icosaedrică.
• Scheletele calcaroase ale radiolarilor au forme foarte diferite, inclusiv solide platonice.

literatură

• Paul Adam, Arnold Wyss: Solidele platonice și arhimedeice, formele lor stelare și structurile polare. Editura Free Spiritual Life, Stuttgart 1984, ISBN 3-7725-0965-7 .
• Renatus Ziegler: Solidele platonice. Relații, metamorfoze, inversiuni. Verlag am Goetheanum, Dornach / Elveția 2012, ISBN 978-3-7235-1326-2 .
• Ilka Agricola , Thomas Friedrich : Geometrie elementară. Expertiză pentru studii și lecții de matematică. Springer Spectrum, ediția a IV-a 2015. ISBN 978-3-658-06730-4 , doi: 10.1007 / 978-3-658-06731-1 .

Link-uri web

• Euclid: Stoicheia. Cartea XIII.18. Marginile celor cinci poliedre diferite inscripționate cu sfere de același diametru
• Foi de ambarcațiuni pentru solidele platonice
• Mediul de învățare Solidele platonice de la Universitatea din Bayreuth

Dovezi individuale

1. ↑ Thomas Digges : Nova corpora regularia: Quinque corporum regularium simplicium ... (Bazat parțial pe „Pantometria” lui Leonard Digges care a fost completată și publicată de Thomas Digges). 1634 ( previzualizare limitată în căutarea Google Book)
2. ↑ Christophorus Leibfried: Tabula III. Orbium Planetarum Dimensiuni and Distantias Per Quinque Regularia Corpora Geometrica Exhibens
3. ^ ^{A b} Wolfram MathWorld: Tetraedru regulat
4. ^ ^{A b} Wolfram MathWorld: Cube
5. ^ ^{A b} Wolfram MathWorld: Octahedron obișnuit
6. ^ ^{A b} Wolfram MathWorld: Dodecaedru regulat
7. ^ ^{A b} Wolfram MathWorld: Icosahedron regulat
8. ↑ Renatus Ziegler: Corpuri platonice - relații, metamorfoze, inversiuni. Dornach 2008, p. 10.
9. ^ Euclid: Elementele. Cartea XIII, § 18a.
10. ↑ Numărul suprafețelor este de două ori mai mare decât numărul. a muchiilor împărțite la p , cele ale colțurilor de 2 ori numărul. a muchiilor împărțite la q
11. ↑ Harish Chandra Rajpoot: unghiuri solide subtinse de solidele platonice (poliedre regulate) la vârfurile lor. SlideShare, martie 2015, accesat la 16 iunie 2020 . 
12. ↑ Eric Weisstein: Dodecaedru. Umkugelradius, formula (17) simplificată în continuare. În: MathWorld Wolfram. A Wolfram Web Resource, accesat la 1 iulie 2020 . 
13. ↑ Eric Weisstein: Dodecaedru. Raza bilei de margine, formula (19). În: MathWorld Wolfram. A Wolfram Web Resource, accesat la 1 iulie 2020 . 
14. ↑ Eric Weisstein: Dodecaedru. Raza în sfera, formula (15). În: MathWorld Wolfram. A Wolfram Web Resource, accesat la 1 iulie 2020 . 
15. ↑ Mike Zabrocki: HOMEWORK # 3 SOLUTIONS - MATH 3260. (PDF) Universitatea York, Matematică și Statistică, Toronto, 2003, p. 4 , accesat la 31 mai 2020 . 
16. ^ Wolfram MathWorld: Tetrahedral Graph
17. ^ Wolfram MathWorld: Cubical Graph
18. ^ Wolfram MathWorld: Octahedral Graph
19. ^ Wolfram MathWorld: Dodecahedral Graph
20. ^ Wolfram MathWorld: Icosahedral Graph
21. ↑ Eric W. Weisstein : Solid platonic . În: MathWorld (engleză).
22. ↑ Eric W. Weisstein : Pentachor . În: MathWorld (engleză).
23. ↑ Eric W. Weisstein : Tesseract . În: MathWorld (engleză).
24. ↑ Eric W. Weisstein : 16 celule . În: MathWorld (engleză).
25. ↑ Eric W. Weisstein : 120 de celule . În: MathWorld (engleză).
26. ↑ Eric W. Weisstein : 600 de celule . În: MathWorld (engleză).
27. ↑ Eric W. Weisstein : 24 de celule . În: MathWorld (engleză)., Delimitat de 24 de octaedre (tridimensionale), 96 de suprafețe triunghiulare, 96 de margini și 24 de colțuri.
28. ↑ Oliver Knill, Cercul de matematică nord-est, Departamentul de matematică Harvard Pagina principală: poliedre și politopi
29. ↑ Martin Pfiffner: Team Syntegrity - Calea cibernetică spre luarea deciziilor în organizații . Malik on Management, 5/2001, pp. 82-95. Online sub Copie arhivată ( Memento din 31 ianuarie 2012 în Arhiva Internet )